|
카오스, 주식시장, 머신러닝 매매
☐ 요점
○ 주식시장은 예측이 가능한 영역인가.
- 시장에 참여하고 있는 모두가 과거에 한 때 품었거나, 현재 가지고 있을 이 질문에 대해 의견을 제시한다.
○ 카오스와 랜덤은 커다란 차이가 있다.
- 카오스 현상은 예측을 할 수 있지만,
- 랜덤 현상은 예측이 불가능하다.
○ 통계만을 이용해서 카오스 프로세스를 모델링하는 것은 가능하지만, 매우 어려운 작업이다.
○ 머신러닝을 사용할 경우, 카오스 프로세스를 보다 효율적으로 모델링할 수 있다.
○ AI와 머신러닝을 통해 주식시장을 예측하고자 하는 시도가 진행되고 있다.
☐ 카오스 vs. 랜덤
○ 카오스와 랜덤의 개념 차이는 해당 성질을 가진 현상에 대한 예측 능력에 있어서 매우 중요하다.
○ 랜덤 이벤트는 이전에 발생한 어떤 이벤트에도 의존적이지 않기 때문에 예측할 수 없다.
- 동전을 던졌을 때 일곱 번 연속으로 앞면이 나왔다고 가정해 보자. 여덟 번째 다시 앞면이 나올 확률은 얼마인가? 여전히 50%이다. 이러한 프로세스는 시간에 따른 통계 속성의 변화가 없으므로 예측할 수 없다.
○ 카오스는 어떤 시스템이 실제로는 결정론적 법칙에 의해 변화하고 있음에도 불구하고, 매우 복잡/불규칙/불안정한 행태를 보이고 있는 현상이다.
○ 훈련되지 않은 사람들의 눈에는 세상의 사건들이 랜덤 이벤트로 보일 수 있지만, 자세히 들여다보면 많은 경우 카오스에 해당한다는 것을 알게 된다.
- 지진, 인구 증가, 주식 시장과 같은 것은 모두 카오스 시스템의 사례이며 합리적인 정확도로 예측할 수 있다.
○ 카오스 프로세스는 세 가지 패러다임에 의해 제어된다.
- 안정성, 기억, 돌발적이고 극단적인 변화
○ 주식시장의 안정성은 주가의 상승추세 또는 하락추세의 형태로 나타난다.
- 추세가 형성되면, 해당 기간 동안 주가는 변하지만 추세는 변하지 않는다.
- 주식시장의 불안감은 추세가 약화될 때 발생한다.
- 주가가 오랜 기간 계속 상승하면 과연 현재의 상승추세가 언제까지 지속될 수 있을지에 대해 의문을 품기 시작하는 시점이 온다.
- 사람들이 그 추세에 대한 자신감을 잃기 시작하면서 안정성은 감소한다.
- 안정성이 감소하면, 작은 사건조차 추세를 완전히 뒤집을 수 있을 정도의 위력을 발휘할 수 있다.
- 이는 임계점에 이른 모래더미에 한 알의 모래가 더해져서 결국 더미를 붕괴시키는 모래사태 모형으로 설명될 수 있다.
○ 기억은 과거의 사건들이 현재의 추세에 미치는 영향이다.
- 한동안 상승해온 주식은 앞으로도 계속 상승할 것처럼 보인다.
○ 사전에 유의미한 경고 없이 추세를 완전히 역전시키는 급격한 변화도 발생할 수 있다.
- 1970년대 이후 금융시장을 뒤흔든 대사건은 10년에 1~2회 정도 발생했다. 이런 예상치 못한 사건을 `검은 백조`, 즉 블랙스완이라고 한다.
- 블랙스완을 예측할 수는 없지만 미래를 예측하는데 유용하다.
- 카오스 프로세스에서 발생하는 상승과 하강 추세의 주기는 다양하며, 안정된 시기 이후 갑작스러운 큰 변동이 뒤따를 수도 있고 그 반대의 경우도 있다.
- 이러한 특성은 확률적 접근을 통해 카오스 시스템에 대한 예측을 가능하게 한다.
☐ 통계를 이용한 카오스 모델링
○ 수학만을 사용하여 카오스 시스템 모델을 만드는 것은 부분적으로 나비효과 때문에 어렵다. 매개변수의 작은 차이가 결과에 급격한 변화를 일으킬 수 있기 때문이다.
○ 다만, 주식시장에서 볼 수 있는 점진적인 추세의 출현과 돌발적 사건의 희귀성은 "1/f 노이즈 모델"을 이용해 모델링할 수 있다.
○ 1/f 노이즈 모델의 기본 원리는 사건의 크기가 빈도에 반비례한다는 것이다. 즉, 사건이 자주 발생할수록 시스템에 미치는 영향은 작아진다.
○ 1/f 노이즈는 시스템에 대한 갑작스러운 충격 또는 개별적이지만 상호 관련된 프로세스의 복합적인 작용에 의해 발생된다.
- 대부분의 경우 원인과 결과에 대한 상관관계가 단순하지 않으며 각 요소는 다른 요소(들)에 의해 영향을 받을 수도 있다.
- 여러 자연현상과 사회현상에서 1/f 노이즈가 관측되는데, 위와 같은 이유로 그 원인을 정확히 파악하는 것은 쉽지 않다.
- 이와 같이 1/f 노이즈는 "랜덤 화이트 노이즈"와 "랜덤 워크 노이즈"의 중간 형태이며, 실제 카오스 프로세스에서 1/f 노이즈는 빈도에 영향을 받지 않는 랜덤 (화이트) 노이즈와 중첩된다.
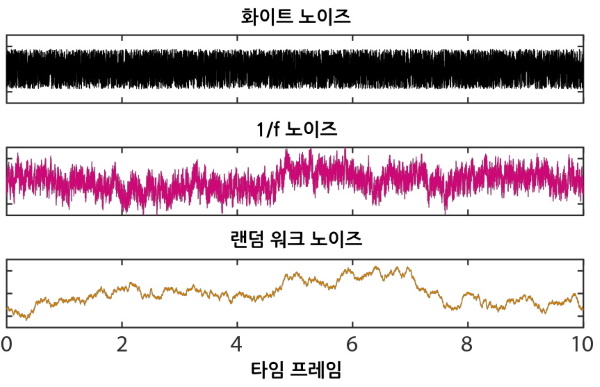
○ 카오스 프로세스에서는 과거의 사건이 현재와 미래의 사건에 영향을 미친다.
○ 수학에서 시계열의 시차 값(과거 값과 미래 값) 사이의 관계를 자기 상관성이라고 한다. 랜덤 프로세스에 대한 자기 상관성은 빠르게 사라지지만 카오스 프로세스에 대해서는 예측에 사용할 수 있는 일정 수준의 지속성을 가진다.
○ 다양한 스케일을 적용해서 카오스 프로세스를 보면 규모에 관계없이 비슷한 패턴을 유지하고 있음을 알 수 있다.
- 이런 자기 유사성은 일부 작은 조각이 전체와 비슷한 기하학적 형태를 갖는 프랙탈 구조에서도 찾을 수 있다.
○ f(x)=ax-k 라는 함수가 있다고 하자. x를 c라는 상수로 스케일링하면 원래 함수도 그에 비례하여 스케일링된다. 일정한 비율로 멱법칙 상관관계를 스케일링하는 것은 카오스 시스템과 프랙탈 모두에서 볼 수 있는 자기 유사성을 유발한다.
○ 자기 유사성은 로그 스케일 그래프에서 f(x) 로그와 x 로그 사이의 선형 관계를 살펴볼 수 있게 해 주기 때문에 매우 중요하다. 보정된 범위에서 선의 기울기는 허스트 지수 H에 프랙탈과 랜덤 시계열을 구분하거나 장기기억과정을 찾을 수 있는 값을 제시한다.
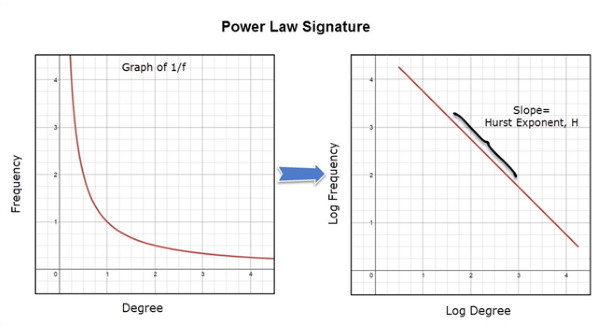
○ 허스트 지수는 시스템의 전반적인 지속성을 측정하는데 사용된다.
○ 허스트 지수 값(H)은 세 가지 경우로 구분하는데, 국내 시장의 H는 개별 주식이 0.6대, 업종별 지수와 전체 시장이 0.7대 정도로 알려져 있다.
① H = 1/2
- 정규분포를 가진 예측 불가능한 랜덤 워크 (브라운 운동) 상태로 시계열 값들 간에 별다른 상관관계가 없음을 의미한다.
② H < 1/2
- 많은 (화이트) 노이즈와 고차원의 프랙탈, 시스템 값들 간의 복잡성이 존재한다. 미래의 추세는 과거와 반대로 진행될 가능성이 크다. 이 경우를 단기기억과정이라고 한다.
③ 1/2 < H < 1
- 중복 노이즈가 적고, 상대적으로 관리가 수월한 저차원 프랙탈이 존재한다. 과거의 추세가 미래에도 유지될 가능성이 크다. 이 경우를 장기기억과정이라고 한다.
○ 또 다른 개념인 MLE(Maximal Lyapunov Exponent)는 허스트 지수와 강한 상관관계를 가지고 있으며 초기 조건에 대한 민감도를 나타낸다.
- MLE는 특정 모델을 실행할 때 입력 값의 조정에 따른 출력 값의 변화, 즉, 분산을 측정한 것이다. 이 프로세스는 입력 변수의 수가 증가함에 따라 복잡해진다.
- MLE의 역(1/MLE)을 이용해서 모델의 예측 능력을 측정하는데, MLE가 클수록 예측력은 감소한다.
- 우리 시장에 대한 MLE는 0에 가까운 마이너스 값으로 알려져 있으며, 해외 시장도 거의 0에 수렴한다. 이에, 주식시장에서 초기 조건에 대한 민감도는 낮다고 봐야 하며 주식시장은 프랙탈 특성을 가진 카오스에 해당하기에 특히 **단기** 예측은 가능하다고 할 수 있다.
○ 프랙탈 시계열의 특성은 카오스 프로세스를 추정하는 데 사용된다.
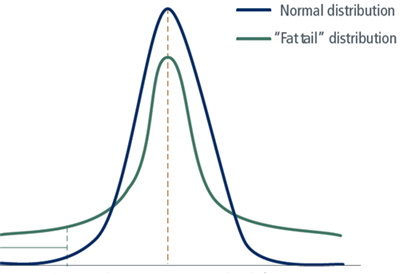
- 정규분포는 평균값이 고정되어 있으므로 자기유사성을 지닌 데이터 세트를 정량화하기에는 적합하지 않다.
- 따라서, 프랙탈 파동의 경우에는 팻테일(Fat-Tailed) 확률분포를 사용한다.
- 팻테일 확률분포에서 분산은 프랙탈 차원(D)으로 특징되는 일부 불규칙성을 나타내는 반면, 평균은 허스트 지수(H)로 특징되는 전반적인 지속성을 나타낸다.
- 팻테일은 자연과 사회에서 극단적인 사건의 발생 확률을 나타낸다.
☐ 알고리즘을 이용한 카오스 모델링
○ 통계를 이용한 카오스 모델링은 상당히 복잡한 작업이다. 이러한 유형의 문제들을 좀 더 수월하게 풀기 위해 우리는 컴퓨터를 활용한다. 특히, 인공지능과 머신러닝은 카오스 구조들을 모델링하고 예측하는데 매우 성공적인 것으로 입증되었다.
○ 머신러닝의 목적은 일반화를 하는 것이다.
- 일반화라는 것은 "새로운 데이터에 대한 모델의 예측성능을 향상하는 작업"이라고 이해하면 된다.
- 기계는 방대한 양의 데이터를 수집하고, 데이터 내에서 규칙을 찾은 다음 이에 기초하여 결과를 예측할 수 있다.
○ 결론적으로, 시계열로 표현한 대부분의 주가 흐름은 전형적인 카오스 현상이므로 머신러닝 기법을 사용하여 그들의 미래 움직임에 대한 예측을 할 수 있다.
|